• ToC

One of the fundamental building blocks for such a system is digital signatures.

Satoshi Nakamoto

One begins to think with that new building block, rather than with littler pieces. And finally, the things which seem like elements dissolve, and leave a fabric of relationships behind, which is the stuff that actually repeats itself, and gives structure to [the whole].

Christopher Alexander

It's almost impossible to talk about Bitcoin in any meaningful way without a brief discussion of the building blocks that make Bitcoin work. So while public-key cryptography, digital signatures, hash functions, and peer-to-peer networks aren't among the first topics that come up during a lively cocktail party, these esoteric constructs undoubtedly have a certain charm once adequately understood.

Even though I do not intend to go into any depth regarding the mathematics of these concepts, I believe it is helpful to understand the general idea in some detail. While not everyone will need to learn the ins and outs of elliptic curve cryptography, there are certain things that need to be understood if you want to use Bitcoin properly. If you're going to take ownership of your bitcoin, for example, you will need to learn what a private key is—which brings us to the first fundamental building block of Bitcoin: public-private key pairs.

Public-key Cryptography

Public-key cryptography, also known as asymmetric cryptography, is at the root of all modern cryptographic protocols, including Bitcoin. As James Dale Davidson and William Rees-Mogg argue in The Sovereign Individual, it is this set of mathematical tricks that is behind a fundamental shift of power dynamics in our world. 

The basic principle is as follows: based on a secret, you generate a pair of keys - one public, one private. These keys are asymmetric, meaning that if you lock the door with one of them, you have to use the other one to unlock it.

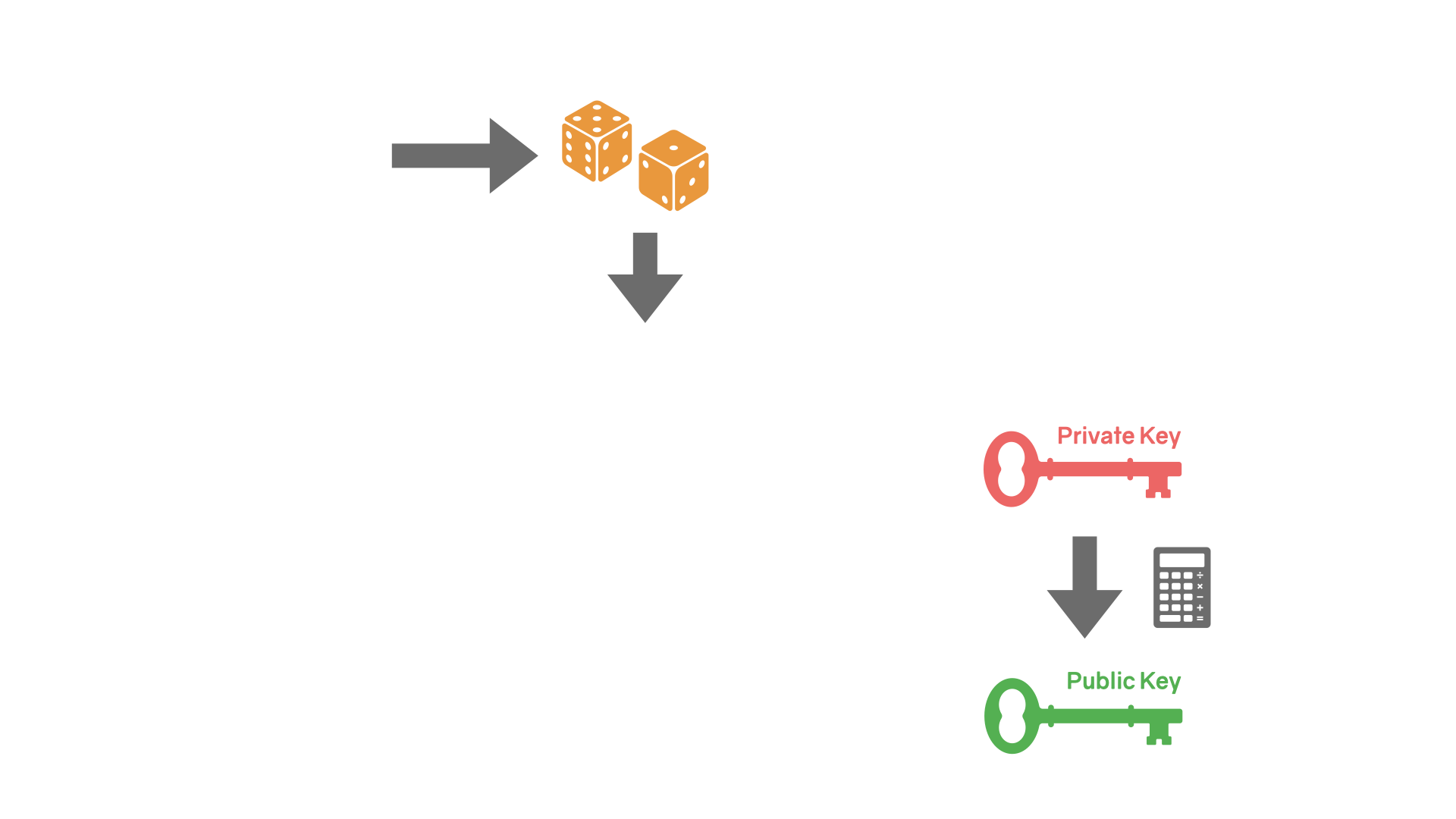
Of course, these keys aren't physical keys, and we aren't talking about physical doors. The keys are data, the doors are algorithms, locking means encrypting (scrambling the data), and unlocking means decrypting (unscrambling the data). Further, the information that is encrypted—or signed, as in Bitcoin's case—is data as well.

All modern cryptography systems are transparent systems. They are built in a way that ensures that the system is secure, even if your enemy knows everything about the system except your personal secret.¹ Bitcoin is such a transparent cryptography system, even though it doesn't encrypt any data. In terms of cryptography, all that Bitcoin makes use of are cryptographic hashes and digital signatures, both of which are distinct from encryption. There are no secrets in Bitcoin. The only secret is your personal secret, which is your private key. As long as you manage to keep your private key secure, your bitcoin funds will be secure as well.

To summarize: public-key cryptography is used to create two numbers that are mathematically linked. One number is shared with the public; the other is not. We call the secret number a private key and the shared one a public key. Bitcoin is a modern cryptographic system that uses these keys.

In Bitcoin, you use your private key to sign messages, which brings us to the next building block.

Digital Signatures

In general, a signature is useful if it is easy to create, easy to verify, and secure from forgery. Signing a physical document usually implies that the document was read and understood by the person who signed it, and the signature authenticates not only the document—making sure that the document is not altered after the fact—but also the signer.

In the world of bits and bytes, thanks to public-key cryptography, the same can be achieved with digital signatures.

A digital signature is the outcome of a special mathematical function that can be applied to data. A user, let's call her Alice, can use her private key to sign an arbitrary message, and other users—everyone, really—can use Alice's public key to verify that she, and only she, created that signature.

A proper digital signature scheme ensures:

• data integrity: ensuring that what was signed has not been altered,
• authentication: ensuring that it was the signer who signed it,
• and non-repudiation: ensuring that the signer can not deny having created the signature after the fact.

In other words, digitally signing a message binds the identity of the sender to the message itself, just like a regular signature binds a person to a document. Thanks to cryptography, however, the guarantees that come along with a digital signature are way stronger than the guarantees of a physical signature. It is virtually impossible to forge a digital signature that was created by a strong signature scheme. In addition to these strong integrity and authentication guarantees, a digital signature is easy to create and verify.

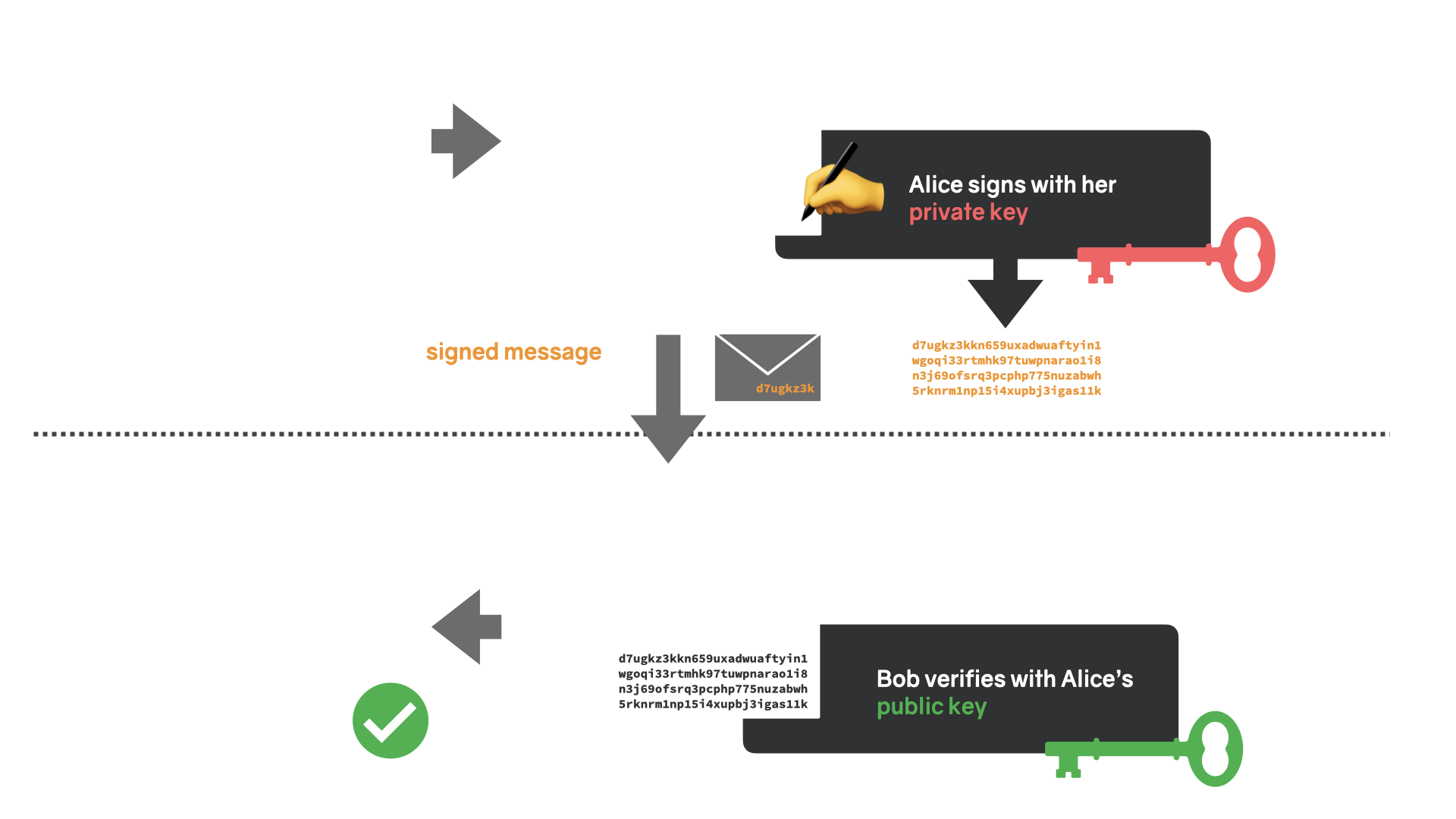
To summarize: digital signatures are used to verify that a message was created by a known sender and that the message was not altered in transit.

In Bitcoin, digital signatures are used to sign transactions. Only valid transactions will be hashed and bundled into a block, and only valid blocks will be hashed so they can be added to the existing chain of blocks. This brings us to the next building block: hash functions.

Hash Functions

A hash function is a one-way function that takes an input of arbitrary length and computes a "fingerprint" that has a fixed length. A hash function is also called a "trapdoor" function because it is easy to fall through a trapdoor but impossible to get back out again. Similarly, it is easy to compute the hash of a piece of data but impossible to compute the original, unscrambled content of said data from that hash alone.

$ echo "Satoshi Nakamoto" | sha256sum 
2662d47e3d692fe8c2cdb70b907ebb12b216a9d9ca5110dd336d12e7bf86073b

Reverse computation is impossible because the space of valid inputs is way larger than the space of possible outputs, which means, in essence, that information is lost when computing a hash.

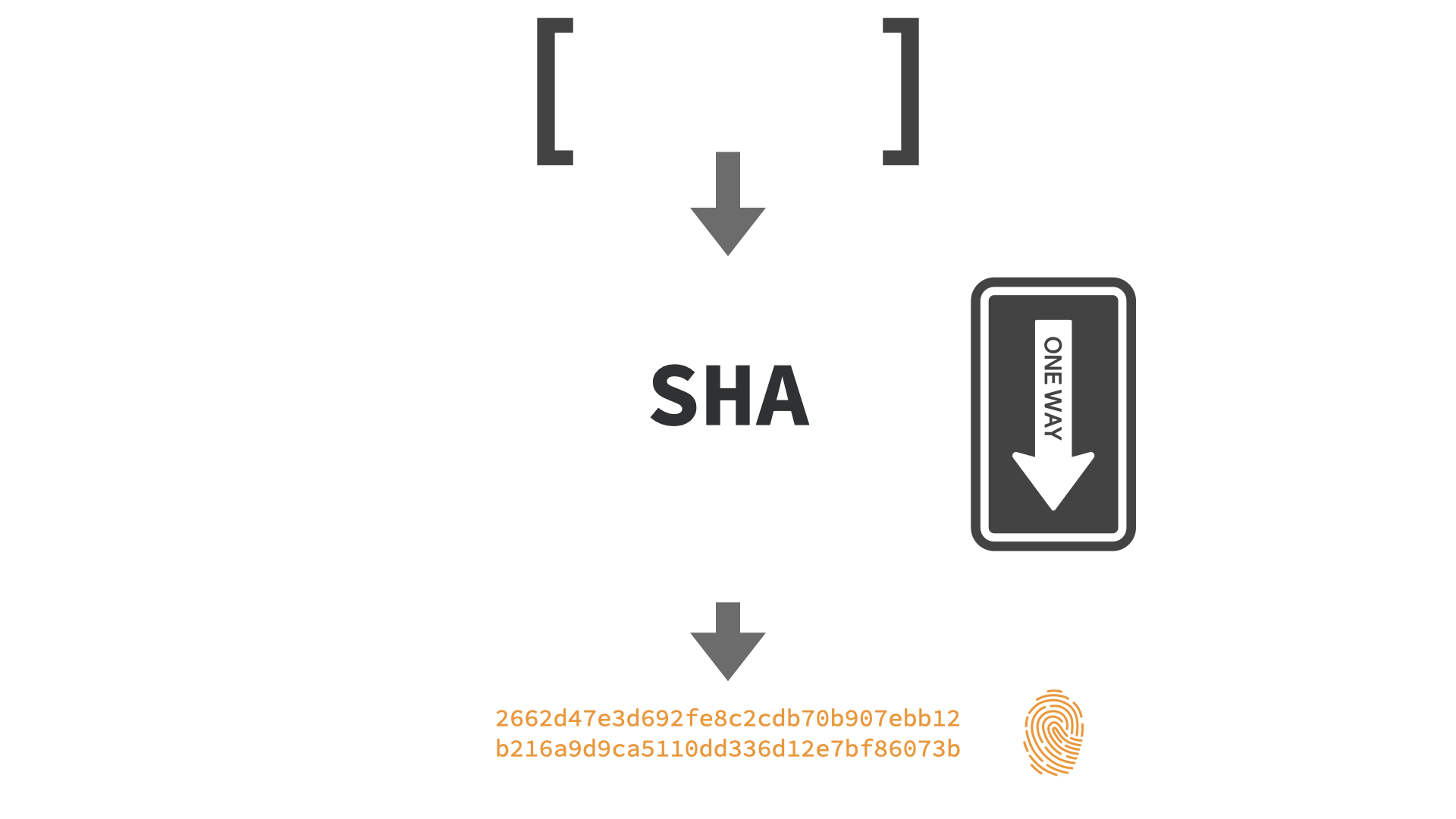
It follows that two different pieces of data can have the same hash. This is what we call a hash collision. The difference between regular hash functions and cryptographic hash functions is how the input data is mapped to the space of possible hashes. Cryptographic hash functions have certain properties that ensure that it is infeasible to find collisions, i.e., two inputs that produce the same output. Additionally, cryptographic hash functions make sure that slightly different inputs produce vastly different outputs, among other things.

In Bitcoin, hash functions are used all over the place. For example: what we call "mining" is the process of trying to find a number that, when put into a potentially valid block, produces an output that fits certain criteria. The SHA256 hash function is what produces this output. Hash functions are also used to generate addresses,² identify redeem scripts, identify transactions and blocks, and more.³

Hash functions are such an important building block because absent of central authority, the data itself is all we have to identify and index information. We can't look up a central index or register that has all the data neatly organized because no such authority exists. This brings us to the last building block: peer-to-peer networks.

Peer-to-Peer Networks

The problem with regular computer networks is a political one. Traditional computer networks usually follow the client-server model, which puts one server in charge as the central authority of the network. Unfortunately, as we have seen in the past, the server does not always serve its clients. More often than not, servers transform into dictators, which is why it is just as fair to use the term "master" instead of "server," and talk not of "clients" but of slaves.

The way out of this conundrum is to make everyone in the network an equal participant by design. Instead of masters and slaves, we have nodes in a network. Equal participants that are not only equally privileged but, more importantly, equipotent in their powers.

That Bitcoin is a peer-to-peer network is of utmost importance. In my opinion, it is the one principle that must be taught and upheld above all others. If we fail to teach and uphold this principle, centralization will inevitably creep in, and with centralization comes central authority. As history has shown over and over and over again, the power that central authority brings with it is too large to be resisted. Inevitably, any central authority will abuse its powers, which is why Bitcoin optimizes for decentralization above all else.

Putting It All Together

As we will see in Chapter 1, a lot of people thought that it should be possible to devise a system for digital money using these building blocks. It turns out they were right, but it took the genius of Satoshi Nakamoto to make it all work.

Bitcoin truly works in mysterious ways. The esoteric building blocks outlined above are game-theoretically glued together to create a self-regulating system unlike any system seen before.

And, as briefly mentioned above, the language to describe this system and its building blocks is terribly inaccurate. We speak of "keys" and "addresses" and "wallets" and "coins" and "transactions" and so on, often forgetting that what we are describing is data and the manipulation of data. With inaccurate language like this, it is all too easy to have an inaccurate picture of Bitcoin's operation in your head.

Alas, there isn't much we can do about this. Language and metaphor are our main tools to make sense of things. Thus, allow me to metaphorically describe a Bitcoin transaction and to correct this description immediately after - with more metaphors, of course. 

Let's say you have some sats in your wallet and want to send 615 sats to Alice. You could think that all you have to do is open your wallet, take out 615 sats, and send them to Alice, just like an attachment of an email.

Well, that's not what's going on. Like, not at all.

First of all, the sats you own are not in your wallet. They are in a transparent vault in the sky, visible to anyone who is willing to look. Your wallet holds the key that unlocks the vault. When you send 615 sats to Alice, you remove your lock from the vault and put Alice's lock on it instead. Now the sats belong to Alice. To send them to Bob, she has to use her key to remove the lock and put someone else's instead, and so on.

But, you ask, wouldn't that transfer all of my funds to Alice? That's right, which is why new vaults are created with every transaction. In this case, one for Alice and one for you to get your change back. Two more details:

1. Your keys aren't physical keys, but magic spells that have to be "spoken."
2. Sats outside of vaults do not exist.

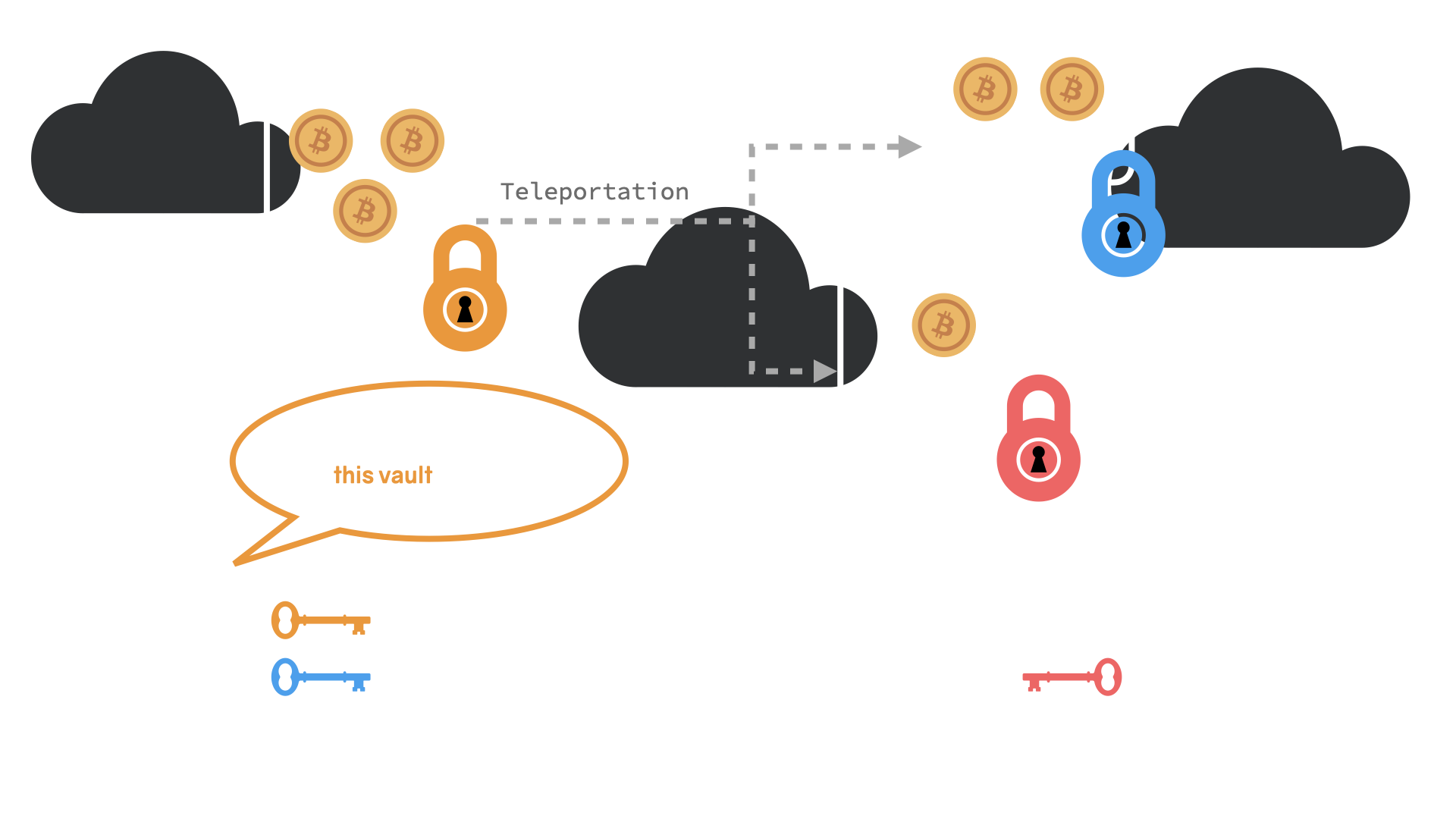
To describe the above in the language of Bitcoin's building blocks: to initiate a transfer of funds, Alice has to use her private key to sign a transaction. One of the outputs of this transaction is Bob's bitcoin address, which is derived from his public key. Once the transaction is signed and broadcast over the peer-to-peer network, Alice's digital signature is checked by everyone. If the transaction is deemed valid, it will eventually be confirmed, and the transfer of funds is complete. Alice's old vault is now empty. Two new vaults were created: one for Alice and one for Bob.⁴

While this picture is again incomplete, it is a somewhat accurate description of what happens when sats change hands. I hope that an ever-clearer image will start to form in your mind over the course of this book. Before we dive into more nuances and technicalities of Bitcoin, let's have a look at Bitcoin's pre-history so we can appreciate its predecessors and origins.

• Bitcoin Is An Idea

Translations

• 🔗 Russian translation by Tony

Want to help? Add a translation!

All translations »

• Chapter Zero
• Table of Contents
• Bitcoin Is An Idea